
볼륨을 가지고 계산하는 방법을 연습해보자.
isooffset을 활용하여 4개의 폴리곤을 볼륨으로 만들어준 뒤 머지로 묶어준다.


Volume Visualization 노드를 달아서 Volume의 각 부분의 밀도가 어느정도 되는지 예측할 수 있도록 diffuse ramp를 활용해 색을 추가해준다.
- 이 색을 통해 현재 Volume의 부분별 밀도를 예측할 수 있어야한다.
- 현재 Diffuse range가 0 / 2 이므로, diffuse field의 1은 diffuse ramp 그래프의 0.5에 해당하는 구간이 된다.
- 보라색은 밀도가 1혹은 1이상의 값을 가지게 될 것이다.
- 모서리 쪽의 노란색은 대략 밀도가 0.25~0.5 사이의 값을 가지게 될 것이다.

밀도값 1은 중요한 값이니까 diffuse ramp에서 밀도값 1인 부분(파랑-보라 경계)을 조금 더 디테일하게 수정해주도록 한다.
- 밀도값 0.95는 하늘색, 1은 남색, 1.05는 보라색으로 디테일을 수정해본다.
- 이렇게 되면, 안쪽의 밀도가 1이어서 보라색인지, 1보다 커서 보라색인지 확인이 가능할 것이다.

보라색 보다는 남색에 가까운 색이 나오는 것으로 봐서 안쪽이 보라색으로 표현되었던 밀도는 1보다 크다고 하기 보다는, 1 언저리의 값이었다는 것을 유추할 수 있다.
a라는 볼륨에 0.5를 곱해주고싶다.
voxel이 가지는 밀도값이 절반으로 줄어들면서 위에 표현된 색이 녹색 위주로 표현될 것이다.
우리가 변환시켜주기 원하는 타겟 볼륨은 a 이다.

그리고 우리가 volume wrangle을 통해 가지고 있는 볼륨도 a밖에 없다.

각각의 볼륨이 가지는 float 값을 이용하기 위해 @a를 사용한다.
@a를 바꿔줄 것인데,
@a = @a * 0.5;
각각의 voxel이 가지고 있는 볼륨 a의 밀도값, 그 float 값에 0.5를 곱해주게 된다.

바깥으로 가면 갈수록 밀도가 0에 가까웠구나 하는 것이 눈에 보이기 시작했다.
wrangle에 chf를 활용해서 사용자가 값을 임의로 변경해줄수도 있다.

Noise를 추가해보자.
noise - 공간상에 존재하는 어떠한 패턴
noise의 패턴에 어떠한 값을 대입했을 때 얻게되는 값을 활용하는 것이 noise의 활용이다.
volume wrangle을 만들어주자.

@a 볼륨을 사용하기 위해서 선언을 해줬다.
noise에는 어떠한 위치정보(@P)가 들어가게 되는데,
- run over가 point 일때는 각각의 point의 위치정보가 들어갔고,
- run over가 primitive 일때는 각각의 primitive의 위치정보가 들어갔다.
- volume wrangle에서는 우리가 이용하고 있는 voxel의 위치정보가 @P로 활용된다.
우리는 이 noise로 얻게 되는 값을 @a에 더해볼 것이다.
@a = @a + noise(@P);
위 식의 의미는 각각의 voxel이 가지고 있는 위치정보를 noise에 대입했을 때 얻게 되는 값을 @a의 float 밀도값에 더해준다는 것이다.
이 식의 결과는 양수가 될수도 있고, 음수가 될수도 있을 것이다.(noise의 패턴에 따라 달라진다.)

결과가 우리가 예측한 것과 조금 다르다. 뭔가 볼륨이 조금 더 커진 느낌이다.
이 부분은 isooffset의 결과에서 바운딩 박스가 얼마나 컸는지 볼 필요가 있다.
확인을 위해 bound 노드를 isooffset에 달아준다.


box를 기준으로 isooffset을 활용해서 볼륨을 생성할 때, isooffset은 판단하기를 박스보다는 좀 더 큰 공간을 만들고 기준이 되는 박스 안쪽은 0보다 큰 어떠한 값으로 밀도를 채우고, 기준 바깥의 공간은 밀도를 0으로 두는 일종의 안전한 구역을 생성한다.
isooffset이 실제 기준이 되는 box보다는 좀 더 크게 볼륨을 만들었었다는 것이 눈으로 확인이 되는 것이다.
다시 노이즈를 더해줬던 volume wrangle을 켜보자.

원래 기준이 되는 box의 바깥의 voxel은 밀도가 0이었다. 그래서 어떠한 값을 곱해주더라도 밀도가 0이었기 때문에 volume visualization을 활용해도 볼 수가 없던 공간이었다. 하지만 noise(@P)가 더해지게 되면서 voxel의 위치정보가 noise에 들어가면서 얻게된 값이 밀도에 더해지게 되었고, 0보다 큰 어떠한 값이 되어서 우리 눈에 묘사가 되는 것이다.
기준이 되는 box 내부 뿐만이 아니라 box 바깥의 밀도가 0이었던 voxel이 보이기 시작하는 것이다.
noise 식을 조금 변형을 해보자. 노이즈를 더해주는 것이 아니라 빼보자.
@a = @a - noise(@P);

기준이 되는 box 내부의 밀도에 노이즈가 살짝 추가된 것도 보이고, 기준 바깥의 voxel의 밀도도 묘사가 되지 않고 있다.
바깥의 묘사되지 않는 voxel도 -noise(@P)에 해당하는 값은 가지고 있다.
안보인다고 해서 정보가 없다는 것이 아니다.
isooffset을 연결했을 때 조차도 밀도가 0이라는 정보를 가지고 있었다. 바운딩 박스 안쪽의 모든 voxel은 정보를 가지고 있었다는 말이다.
Volume VOP으로 noise를 작업해보자.

density를 사용할 것이 아니기 때문에 끊어준다.
우리가 현재 사용하려는 볼륨은 a이다.

위치정보를 활용하기 위해서는 volumevopglobal의 P가 필요하다.
우리가 가지고 있는 모든 voxel의 위치정보에 대하여... 라고 생각하면 된다.(@P에 해당된다.)



만약, add가 아니고 multiply를 해준다면 어떻게 될까?


밀도가 존재하는 구간에 대해서는 노이즈가 곱해진 것이 의미가 있고, 밀도가 0인 구간은 의미가 없다.

volume 컨테이너를 하나 만들어서 한가지만 더 확인해보자.
임의의 포인트를 만들고 voxel과 포인트와의 거리를 활용해서 sphere처럼 표현되는 볼륨을 만들려고 한다.



volume visualization 노드를 활용해 눈으로 보이도록 적용해준 결과이다.
이와 같은 효과를 volume wrangle에서 fit function을 활용해 만들어줄 수도 있다.


둘의 다른 점이 있다면,
volume visualization은 실제 볼륨의 값에 변화를 주지는 않았다. 시각적으로 이 부분에 주목해보겠다 라는 표현을 해준 것일 뿐이다.
volume wrangle에서 fit function을 활용한 것은 실제 볼륨에 들어가게 되는 밀도가 바뀌었다.
이제 서로 다른 볼륨들 끼리에 대한 계산을 해보자.
가장 간단한 사칙연산부터 시작해보자.
서로 다른 두 볼륨을 더한다는 것
볼륨 a와 볼륨 b가 있을 때, 두 볼륨을 더한다는 것은 기본적으로
볼륨 a 더하기 볼륨 b (x)
볼륨 a에 볼륨 b를 더한다. (o)
이처럼 두번째 문장으로 이해하는것이 좀 더 이해가 편하다.
결과로 나오게 되는 것은 a의 해상도에 영향을 받게 된다.
볼륨 a에 볼륨 b를 더할 때는, 볼륨 b에 대해서 볼륨 a의 바운딩박스에 걸쳐지는 구간에 대해서만 관심이 있다.

만약 거꾸로, 볼륨 b에 볼륨 a를 더했다면?

볼륨 b가 기준이 되어서 b의 바운딩박스에 걸쳐지는 볼륨 a에만 관심을 가지고 볼륨 b의 바운딩 박스 바깥 부분은 신경쓰지 않는다.
두 볼륨을 merge로 묶어주면 우리가 이용할 수 있는 볼륨은 a와 b 두가지가 된다.

volume wrangle을 활용해서 @a와 @b를 더해준다.
@a = @a + @b;
결과가 잘 보이지 않기 때문에 blast를 활용해서 @a를 따로 떼어내본다.


거꾸로 @b 에 @a를 더해보는 것도 해보자.
@b = @b + @a;


두 볼륨에 대한 사칙연산을 작업할 때 중간에 merge 노드를 사용했다.
이 merge는 volume wrangle, volume vop에서 연산을 수행할 때, 이 볼륨과 저 볼륨의 정보를 같이 가지고 있다는 것을 알려주기 위한 역할을 할 뿐이다.

merge를 사용하지 않고 바로 volume wrangle, volume vop으로 여러 볼륨의 연산을 수행하기 위해서는 volumesample이라는 새로운 function을 알아야한다.

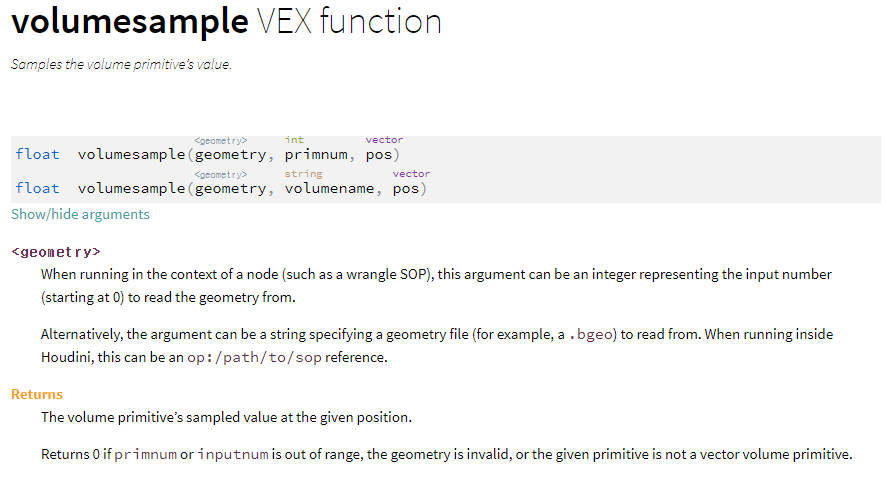
(왜 나는 volumesample을 모를까... 튜토리얼 보면 다 쓰던데 왜 나만 모를까... 이런 상황이 올 수 있다)
volumesample은 point function과 다를바가 없다.
point(1, "b", 0);
'두번째 인풋으로 들어오는 정보에 대해 0번 포인트가 가지는 정보 중 b라는 어트리뷰트를 받아오겠다.' 라는 의미이다.
volumesample(1, "", vector);
내가 가진 각각의 voxel은 현재 두번째로 들어오는 내용 중에서 "" 속에 들어갈 볼륨의 vector에 해당하는 위치의 값이 궁금하다. 라는 의미이다.
ex) volumesample(1, "b", {0,0,0}); 의 의미는, 내가 가진 각각의 voxel은 두번째 인풋으로 들어오는 내용 중에서 볼륨 b의 {0,0,0} 위치의 값이 궁금하다. 라는 의미이다.
좀 더 명확한 예시1 - 선생님 예시

볼륨 A가 오른쪽 그림과 같이 8개의 voxel로 구성되어 있다고 했을 때,
volumesample(1, "B", {0,0,0}); 이라고 한다면,
볼륨 A의 모든 voxel은 볼륨 B가 가지는 {0,0,0}에서의 밀도값을 가지게 된다.
좀 더 명확한 예시2 - 선생님 예시

현재 볼륨 B, C, D, E는 레퍼런스 형태로 들어오고 있기 때문에, 볼륨 A에 아직까지는 아무런 영향을 준 것이 아니다. 그리고, volume wrangle(혹은 volume vop)에서 적극적으로 merge가 되는 스타일이 아니다. 볼륨 B, C, D, E의 정보를 가져와서 해석하겠다는 것처럼 volumesample을 이해하면 된다.
volumesample(1, "D", {2, 1, 0});
내가 가진 모든 voxel들은 궁금해하고 있는 것이 있다. 두번째 인풋으로 들어오는 볼륨 중 D라는 볼륨의 {2, 1, 0}의 위치의 밀도값이 궁금하다는 의미이고, 만약 이 위치의 값이 0.1이라면, 0.1이라는 값을 볼륨 A의 모든 voxel이 알게 되는 것이다.
만약, volumesample(1, "D", @P); 라면?
볼륨 A의 각각의 모든 voxel이 두번째 인풋으로 들어오는 볼륨 D의 본인의 위치정보에 해당하는 위치의 값을 가지게 된다.
세번째 인자(vector)에 {0,0,0} 또는 {2,1,0}과 같은 단일 벡터가 들어간다면, 볼륨 A의 모든 voxel은 볼륨 D의 일정 부분에 대한 밀도값을 가지게 되고, @P를 써준다면 볼륨 A의 각각의 voxel이 가지는 위치를 기반으로 레퍼런스 볼륨 D의 그 위치에 해당되는 값을 불러오게 된다.
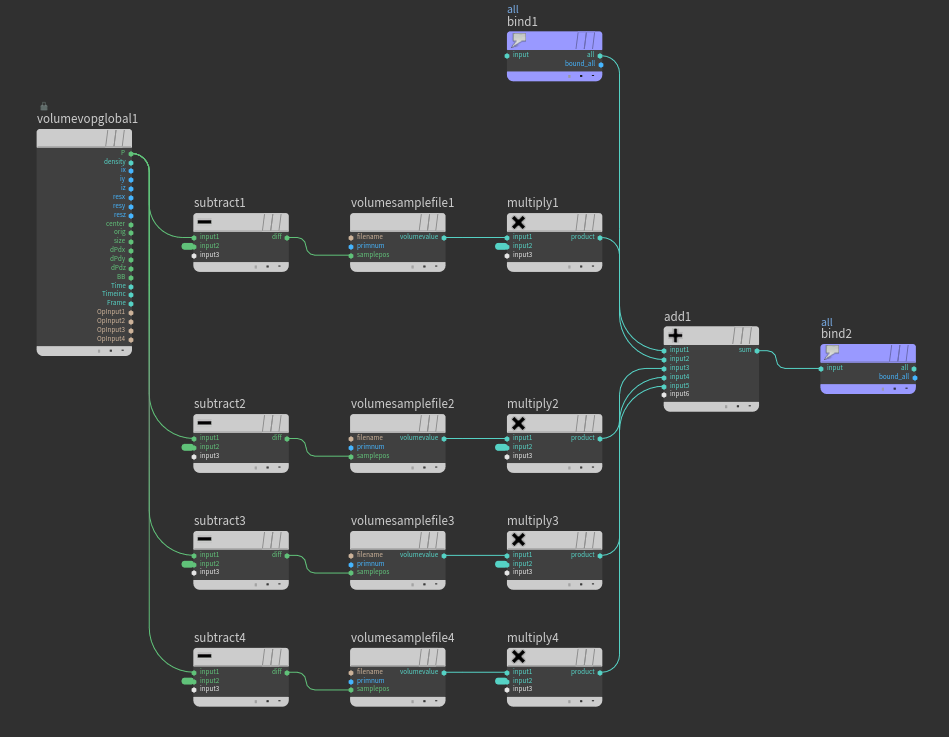
위에서 했던 볼륨끼리의 합을 volumesample을 활용해서 만들어보자.

볼륨 b, c, d는 볼륨에 대한 정보가 있다는 것을 volume wrangle에게 알리기 위해 merge로 묶었다.

우선 볼륨 b의 {0,0,0}에 해당되는 밀도값을 @a의 모든 voxel에 더해보자.

볼륨 a의 모든 voxel에 볼륨 b의 {0,0,0}의 밀도값이 더해진 결과이다.
그렇다면 volumesample에 단일 벡터가 아닌, @P를 적는다면?


기준은 볼륨 a이다. 볼륨 a의 각각의 voxel은 두번째 인풋으로 들어오는 볼륨 중 볼륨 b에 대해서 자신의 위치에 위치하고 있는(겹치는) 볼륨 b의 밀도값을 가져와서 볼륨 a의 밀도값에 더하게 된다. 그렇기 때문에 볼륨 a의 voxel이 없는 바운딩박스 바깥은 버려지게 되고, voxel이 겹치는 구간의 밀도값을 가져와서 더하게 되는 것이다.


그렇다면, 각각의 볼륨형태를 모두 가지고가면서 더해주고 싶다면 어떻게 하면 될까?
- 형태를 가지고 가기 원하는 볼륨보다 큰 바운딩박스를 가지는 볼륨 컨테이너가 있고, 그것이 메인이 되어서 볼륨의 연산을 적용하면 될 것이다.





위의 내용을 volume vop으로 표현해보자.
volume을 쓰면서 노이즈를 다루게 된다면 volume wrangle보다는 volume vop이 더 편할수도 있다.
노이즈를 쓰는 것이기 때문에 이 부분은 확실히 vop이 편하다.






filename : 인풋 번호를 연결해준다.
- volume sample parameter의 Input 항목에서 선택해줄수도 있다.

primnum : 우리는 현재 볼륨의 이름을 알고 있기 때문에 a, b, c, d와 같이 써줄수도 있지만, prim number를 활용할 수도 있다.
- volume sample parameter의 signature 항목에서 선택해줄 수 있다.


이제 sample position에 변화를 줘보자.

위와 같이 voxel이 있다고 가정하자.(z를 무시하고 x, y로만 표현된 좌표계)

@TWA = @TWA + volumesample(1, "A", @P);
- @TWA의 각각의 voxel의 위치에 대응되는 볼륨 A의 위치의 값을 가져왔다.

vector new = @P + (1, 0);
@TWA = @TWA + volumesample(1, "A", new);
- 새로운 벡터 new라는 것을 만들어주고, 각각의 voxel의 위치에 {1,0}을 더해줬다.
- 이렇게 더해준 new라는 벡터를 volumesample에 활용할 경우, 각각의 voxel의 위치 + {1,0}에 해당되는 위치의 voxel 정보를 가져오게 된다. ( {0,0}은 {0+1, 0+0}, 즉 {1, 0}의 정보를 가져온다.)
- 그렇기 때문에 가져온 voxel의 데이터가 왼쪽으로 당겨진것처럼 보이는 것이다.

vector new = @P + (0, 1);
@TWA = @TWA + volumesample(1, "A", new);
- 새로운 벡터 new라는 것을 만들어주고, 각각의 voxel의 위치에 {0,1}을 더해줬다.
- 이렇게 더해준 new라는 벡터를 volumesample에 활용할 경우, 각각의 voxel의 위치 + {0,1}에 해당되는 위치의 voxel 정보를 가져오게 된다. ( {1,0}은 {1+0, 0+1}, 즉 {1, 1}의 정보를 가져온다.)
- 그렇기 때문에 가져온 voxel의 데이터가 아래쪽으로 당겨진것처럼 보이는 것이다.


{1,0,0}을 더해줬더니 마치 volumesample에 의해서 {-1,0,0}만큼 움직인 것 처럼 보인다.

일정이상 값이 커져서 컨테이너 바깥으로 나가면 볼륨이 잘리게 된다. 컨테이너가 같이 커지는 것이 아니다. 컨테이너를 기준으로만 보여주게 된다.
- 거꾸로 움직이는 것이 헷갈린다면, wrangle의 식에서 chv를 더해주는 것을 빼주는 것으로 바꾸면 된다.
위 식은 한번 더 변형이 가능하다.

이제 volume vop으로 표현해보자.



위치를 옮기는 것은 transform을 활용해서도 가능하다.
하지만 그것은 이미 만들어진 볼륨을 어느 위치에 두느냐에 대한 것이다.
위의 방식으로 위치를 움직이는 것은 실제 볼륨 데이터를 다루는 상황인 것이다.
요약.


위와 같은 식을 통해서 컨테이너 볼륨 twa를 채워줄 것이다.
이 때, move라는 vector 변수에 따라 불러들어온 volume의 위치가 바뀌었다.
실제 레퍼런스 볼륨의 위치는 컨테이너의 가운데에 위치하고 있다.
그런데, move 값에 의해서 볼륨의 위치가 바뀐 것이다.
이제 표현을 바꿔보자.(뉘앙스가 바뀐다.)
twa 컨테이너가 d라는 볼륨을 원래의 위치에 불러올 예정이다.
그런데 각각의 voxel들은 vector move라는 값을 가지고 불러들인 밀도값을 이동시킬 것이다.
'twa라는 컨테이너의 각각의 voxel들이 밀도의 위치를 이동시킨다.' 라는 뉘앙스가 필요하다. 어디로 이동시켰느냐? vector move 값만큼 모든 밀도의 위치를 이동시킨 것이다.
이것은 각각의 voxel이 가지는 vector move 값이 서로 같기 때문에 밀도를 한번에 이동시킨 것으로 보이는 것이다.
그렇다면, 각각의 voxel이 가지는 vector move 값이 서로 다른 경우엔 어떻게 될까?
- 볼륨의 모양 자체가 바뀌어버릴 수 있다.
noise를 활용해보자.


channel vector를 사용하는 대신, move에 @P를 활용한 noise function을 적용하였다.
현재 레퍼런스 볼륨은 twa 컨테이너(박스형태)의 가운데에 위치하고 있다.

모양의 왜곡이 일어나기 시작했다.
volume vop으로도 확인해보자.



노이즈의 amplitude를 2로 올리고, 해상도를 더 높여보자.

이 상태에서 turbulent noise의 roughness를 올려준다면 어떻게 될까?


표현이 거칠거칠해진다.
숙제 아닌 숙제
구름을 만들어보자.

오늘 강의에서는 다행히도(!) 막히거나 하는 부분은 없었던 듯 하다(!!!)
그래서 더 불안하다(...!)
그럴리가 없는데...? 마치 디버깅 없이 쭈욱 코딩하고 돌렸는데 에러 하나 안뜨는 상황에 직면한 그런 느낌?
어? 그럴리가 없는데...?
이런 느낌이다...
volumesample이 이해가 되어서 그런가보다 라고 좋게 좋게 생각하기로 했다. 하하하...
'Houdini > Houdini1_Volumes' 카테고리의 다른 글
| 05_볼륨의 확산? 이류? VOLUME ADVECT (0) | 2023.02.22 |
|---|---|
| 04_Vector Volume / VOL TRAIL, GRADIENT, CURVATURE 🔥완전중요🔥 (1) | 2023.02.21 |
| 03_VOLUME_part2. Volume 계산능력 향상 필수 (0) | 2023.02.17 |
| 02_VOLUME NODE 다루기 & 시각화 (0) | 2023.02.15 |
| 01_VOLUME 기초 이론, DENSITY와 SDF(Signed Distance Field) (0) | 2023.02.14 |



