
오늘 다룰 주제.
1. vector volume & how to visualize
지금까지 다룬 밀도값을 가진 볼륨은 눈으로 시각화해서 보기가 좋았는데, 벡터 볼륨은 다른 방식이 필요하다.
2. Couverture & Gradient
3. Advect
확산에 대한 내용 / VDB Advect
4. Volume with Solver
일반 solver와 volume의 활용
5. Particles with vector field
파티클이 움직이는 조건을 우리가 만들어준 볼륨(Vector field)이 될 수 있도록 해줄 예정이다.

vf(Vector Field)라는 이름의 볼륨을 만들어줬다.
- 이 볼륨에서 보고 싶은 것은 밀도로써의 정보가 아닌, 방향으로써의 정보이다.
- 각각의 voxel이 가지고 있는 방향이 어디인지가 궁금한 것이다.
- volume visualization 노드를 활용해 vf를 보는 것은 큰 의미가 없다.
Volume Trail Node
- 주어지는 포인트의 위치를 기준으로 볼륨이 가지는 방향에 따라 시각적으로 묘사되는 노드

- 첫번째 인풋
- 포인트의 정보가 연결
- 두번째 인풋
- 분석하고 싶은 볼륨의 정보가 연결

velocity volumes
- 어떤 vector field를 사용하고 싶은지 표기
- vector field의 쪼개진 volume(vf.x, vf.y, vf.z)을 사용한다고 하면 1차원 볼륨을 사용하게 되는 것이고 vf.*을 사용한다고 하면 3차원 볼륨을 사용하는 것이다.


volume trail을 확인해보기 위해 위와 같이 세팅해줬다.
box에 isooffset을 적용해서 볼륨으로 만들어주고, scatter로 점을 뿌려줬다.

volume trail의 첫번째 인풋으로 넣어준 포인트들 중에서 vector field에 영향을 받은 포인트만 trail이 묘사되었다.
- 흐르는 선으로 표현된 것은 volume vop으로 turbulent noise를 적용해준 것을 시각화한 것이다.
- 현재 전반적으로 흐르는 방향성이 대각선 방향으로 나타나는 이유는 turbulent Noise가 0~1사이의 벡터값을 반환하고 있기 때문에 평균적으로 {0.5, 0.5, 0.5}의 방향으로 흐르게 되는 것이다.

노이즈의 frequency가 증가하면 증가할수록 자글거림이 심해지고, 감소할수록 완화된다.


Volume Slice Node
- 볼륨을 잘라서 단면을 볼 수 있도록 해주는 노드
- volume trail 적용시 안이 너무 빽빽해서 확인이 어려운 경우가 존재함. 이런 때 볼륨을 잘라서 단면을 보고 분석할 수 있도록 해줌
- volume slice로 보게 되는 각각의 사각형은 실제 voxel의 size와 동일하다.
- 정보를 제공함에 대해 scatter로 뿌려주는 점의 갯수를 조절하는 것과, volume slice를 활용하는 부분은 차이가 날 수 있다.
- volume slice를 활용하게 되면 알아서 해상도에 맞는 포인트의 갯수를 활용하게 된다.
- 해상도에 높으면 높을수록 volume slice가 제공하게 되는 point의 갯수가 많아지게 되면서 빼곡해보일 수 있다는 문제는 있다.
- attribute wrangle로 랜덤성을 부여해서 포인트를 지워줄 수도 있고 그러하다.
- 정보를 제공함에 대해 scatter로 뿌려주는 점의 갯수를 조절하는 것과, volume slice를 활용하는 부분은 차이가 날 수 있다.


위의 결과는 volume slice가 잘라놓은 단면을 기준으로 volume trail을 생성한 것이다.

Offset - volume slice 단면의 위치를 조정 가능
Plane - slice하게 되는 단면의 축을 바꿀 수 있다.
volume trail에서 가장 중요한 것은 어떤 볼륨을 분석할것인가?
두번째 중요한 것은 Advection Method - 어느 방식으로 trail을 보기 원하는지에 대한 항목

Advect by Distance
- 앞으로 장차 나아갈 수 있는 방향을 따라 일정거리(Trail Length)만큼 경로가 표현

Advect by Time
- 주어진 시간에 얼만큼이나 경로를 따라갈지 묘사하는 방식
- Time일 때의 Trail Length는 거리 개념보다는 시간 개념으로 이해하는 것이 낫다.
- trail length가 길다 > 시간이 길다
- trail length가 짧다 > 시간이 짧다

ex) Advect by Distance를 이용한다면, 경로를 trail length만큼 모두 그려보게 된다. trail length가 길어지면 무한정 길어지게 된다.
Advect byTime을 이용한다면, 노란구간(상대적으로 세게 표현되는 곳들)은 경로가 많이 나오게 된다.(세다는 것은 같은 시간 안에 더 많이 뻗어나가는 것을 의미하기 때문이다.)
정리
volume slice와 volume trail
둘 중에서는 volume trail이 조금 더 중요하다고 생각.
volume trail의 첫번째 인풋(포인트의 정보)을 어떻게 주느냐에 따라 어느 곳의 벡터 정보를 시각화할지 정해줄 수 있다.
volume slice
우리가 가진 볼륨을 단면화함으로써 시각화를 도와줌
이 때 얻게 되는 결과는 Grid와 같은 형태, volume trail의 포인트 정보로 활용된다면 시각화 가능
Noise와 SDF의 결합
Curl Noise
- SDF를 동시에 활용할 수 있는 Noise
- 자동으로 SDF를 Noise와 결합시켜주는 기능이 있다.
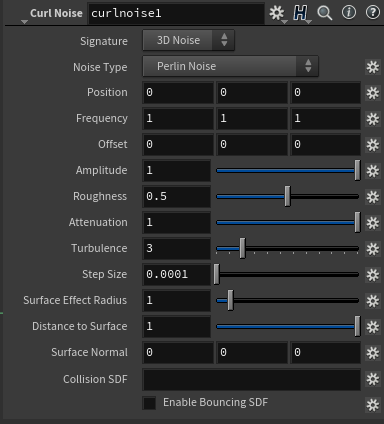

Override Bounds
- 어느 영역 안에서 인풋으로 받은 폴리곤을 SDF volume으로 바꿀 것인지 정해줄 수 있게 된다.
Noise의 발전
Noise function이 생겨난 초창기부터 지금까지 어떠한 형태로써 계속 진화를 해왔을 것인데, parameter를 확인해보면 어떤식으로 업그레이드가 되어왔는지 유추가 가능하다.
Periodic Noise
굉장히 심플한 parameter 항목들
Noise Type도 두개 뿐이다.(Perlin, Simplex)
frequncy, offset 등이 없어서 포지션에 대한 정보를 바꾸는 것이 쉽지 않다.
흐름(flow)에 대한 개념이 없다.
기본적으로 0~1사이의 어떠한 패턴이 존재한다.(전반적인 평균이 0.5라는 경향을 갖게 된다.)

Flow Noise
굉장히 심플한 parameter 항목들

Anti-Aliased Noise
Noise 패턴을 좀 더 쉽게 조절할 수 있도록 다양한 parameter가 생김
패턴에 대한 경향성에 어느정도 보정이 들어갔다.
- 기본적으로 0을 기준으로 +/- 로 결과가 나오게 된다.
위치정보 / 방향에 대한 노이즈 활용에 좋다.
마이너스 값이 표현에 지장을 주는 경우에는 문제가 생긴다.(ex - pscale, alpha)

Turbulent Noise
Anti-Aliased Noise가 공간상에서는 장점을 보이지만 스케일같은 값에서는 음수값으로 인해 단점으로 작용하기도 했다.
Turbulent Noise의 기본은 0~1 사이의 값이 된다.
Anti-Aliased Noise보다 좀 더 다양한 Noise Type을 가지고 있다.

Anti-Aliased Flow Noise
Anti-Aliased Noise + Flow Noise
Noise Type을 정하는 구간이 없다.

0~1 사이의 값으로 표현되는 Noise : 스케일에 활용되기 좋음
Periodc Noise, Turbulent Noise
-1~1 사이의 값으로 표현되는 Noise : 공간에 활용되기 좋음
Anti-Aliased Noise, Anti-Aliased Flow Noise, Curl Noise
Curl Noise
공간상의 Noise 표현 + SDF를 다룰 수 있게 됨(0을 기준으로 하는 -1 ~ 1 사이의 값)
아쉬웠던 Noise Type 갯수가 증가했다.





Curl Noise가 SDF를 받아들일 때, 얼만큼 Noise 정보를 만들었는지 확인하는 방법
- SDF가 적용된 Curl Noise에서 SDF가 적용되지 않은 Curl Noise를 빼보면 된다.

SDF가 적용된 것과 적용되지 않은 것에 차이가 없는 부분은 빼주면서 아예 사라졌다(바운딩 박스 모서리 쪽들)
SDF가 있는 쪽으로 들어가면 들어갈수록 점점 빨간색으로 묘사되고 있다.
- 겉부분은 보라색으로 힘이 약하고, 표면에 가까워지면서 빨간색으로 묘사되고 있다.

Surface Effect Radius
- SDF가 Curl Noise에 영향을 주게되는 범위
Volume에서의 Couverture
곡률
곡률이 높다 > 많이 꺾여있다
곡률이 낮다 > 적게 꺾여있다
크다 / 작다 > float 값으로 이뤄진 볼륨정보
Volume에서의 Gradient
볼륨의 normal 정보
방향 정보 > vector 값을 가지는 3차원 볼륨정보
SDF가 커지는 흐름 방향
SDF는 표면과 voxel간의 최단거리에 대한 내용 > float 값
volume trail, volume slice가 시각화에 별 의미없다.(vector 정보가 아니기 때문)
SDF를 분석해보기
- SDF 표면이 가지는 normal 정보를 얻어볼 예정이다.
VDB Analysis Node

Operator : VDB를 분석하는 방식을 정해줄 수 있다.
- Operator가 Gradient라면, Gradient에 대한 정보가 볼륨에 저장이 된다.


Output Name : 볼륨의 이름을 지정해줄 수 있다.
- Keep Incoming VDB Names - 분석한 볼륨의 이름을 그대로 사용하겠다.
- Append Operation Name - 분석한 볼륨에 Operator를 붙인 이름을 사용하겠다.
- Custom Name - 임의의 다른 이름을 사용하겠다.

Gradient operator를 적용한 VDB Analysis의 결과는 Vector로 Volume trail / Volume slice 콤비를 적용할 수 있다.
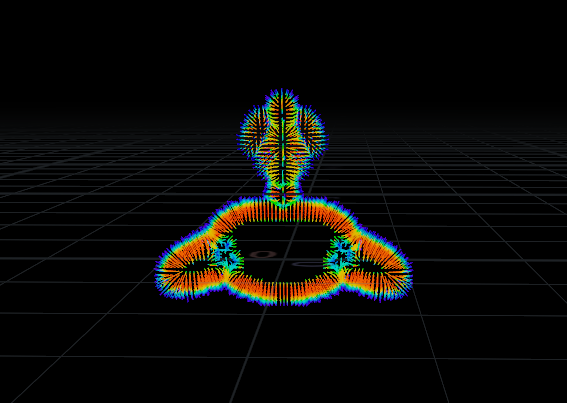

현상적으로는 polygon의 normal에 대한 결과와 유사하다.
- 이것은 표면쪽에서의 이야기이다.
표면이 아닌 곳에서도 어떠한 gradient가 구해진다.
- 표면이 아닌 바깥쪽에서도 gradient가 구해진 것을 확인할 수 있다.

gradient가 어떻게 구해지는가?
표면에 대해 각 voxel에서 표면까지의 최단거리를 구한 것이 SDF다.
이 때, 각 voxel에서 표면을 향하는 최단거리에 대한 vector를 만들고,
- 이 vector를 DF(Distance Field)값으로 나눠주면 표면바깥쪽에서는 안쪽으로, 안쪽에서는 바깥쪽으로 향하게 되는 크기 1의 방향벡터가 만들어진다.
- 이 vector를 SDF(Signed Distance Field)값으로 나눠주면, 표면 안 / 밖의 모든 voxel들에서 안쪽으로 향하게 되는 크기 1의 방향벡터가 만들어진다.(DF값으로 나눴을 때의 안쪽에서 바깥을 향하던 vector의 방향이 바뀐다)
- 이때의 방향은 SDF가 작아지는 방향을 나타내는 것이다.
- 이 vector를 SDF에 -1을 곱해준 값으로 나눠주면, 표면 안 / 밖의 모든 voxel들에서 바깥을 향하게 되는 크기 1의 방향벡터가 만들어진다.
- 이것이 볼륨의 gradient이다.
- SDF가 커지는 흐름의 방향을 나타낸 것이 gradient이다.
- 밀도가 될 수도 있고, 온도가 될 수도 있다. SDF 뿐만이 아니라 float 값이면 다 된다.
- float 값을 가지는 볼륨에서 그 값이 커지는 방향을 구한 것이 gradient이다.
왜 density 볼륨의 gradient는 갑자기 뚝 끊기는 구간이 있을까?




밀도에 대해 gradient를 보겠다의 의미
- 밀도가 커지는 방향을 보고싶다.
- 밀도값에 대한 흐름을 보고싶다.
Couverture
- 일반적인 수학이었다면, 미분으로 곡률을 쉽게 구할 수 있다.
- 하지만, 3d 공간에서는 이야기가 좀 다르다.
- maybe, 세개의 점의 관계를 활용해서 곡률을 유추해낸다.
- 우리는 곡률을 이해하는데 필요한 것은 Analysis를 통해 곡률을 얻었을 때, 이 값이 어떤 결과인지 이해할 수 있으면 되는 것이다.
곡률 값은 양수 / 음수를 갖는다.
- 라인의 봉우리 부분은 안쪽으로 원이 그려지고, 곡률값은 양수이다.
- 라인의 골짜기 부분은 바깥쪽으로 원이 그려지고, 곡률값은 음수이다.
곡률의 값의 크기는 각 봉우리 / 골짜기의 정점에서 가장 크다.(기울기의 부호가 변하는 시점)
곡률값이 제일 큰 지점에서 그리게 되는 원의 반지름은 제일 작다.(곡률값과 원의 반지름은 반비례관계)
Couverture의 정의
- 곡선에 접하는 구의 반지름(r)으로 1을 나눈 값

곡선에 접하는 구가 있을 때, 반지름의 크기(r)를 안다면 곡률을 구할 수 있다.
- 반비례 관계이다.
- 그래야 곡률이 높을 때 많이 꺾이고, 곡률이 낮을 때 적게 꺾인다.
volume에서 곡률을 확인하는게 좀 더 난이도가 있다.
polygon에서의 Couverture
Volume Analysis Node
- 일반 볼륨의 분석에 사용된다.
- VDB Analysis 노드와 다른 점은 이름을 바꿔줄 수 없다. 분석만 가능하다.

Measure Node
폴리곤의 분석에 사용되는 노드

Measure parameter : 무엇을 측정하고 싶은지 선택할 수 있다.


scene view에 바로 변화가 발생하지는 않지만, 우리가 가진 각각의 포인트들에 곡률이 구해졌다.

Curvedness : 곡률의 크기만 나타냄(방향에 대해 나타나지 않음) > 절대값
Principal : 곡률의 크기가 양수 / 음수로 표현됨

폴리곤에서 봤을 때, 밖으로 튀어나온 곳은 곡률이 양수, 안으로 들어간 곳은 곡률이 음수이다.



measure 노드를 선택하고 엔터를 치면 scene view가 measure 모드로 들어가고, 컬러로 시각화된 폴리곤을 확인할 수 있다.


Crag를 활용해서 곡률을 확인해보자.
- 폴리곤이 끊겨있는 구간을 보완하기 위해 crag를 SDF volume으로 변환했다가 polygon으로 convert 해줬다.
- convert VDB를 이용해 다시 polygon으로 바꿔주면서 isovalue 값을 조절해서 SDF 값이 isovalue 값인 곳을 면으로 연결해준 결과이다.

위의 결과에 remesh 노드를 달아서 면이 고르게 분포되도록 해준다.
measure 노드를 달아서 curvature값을 만들어주고, attribute wrangle을 활용해서 색을 추가해준다.


약간의 디벨롭
곡률이 양수로 더 큰 곳(더 튀어나온 곳)은 노란색을 추가해서 강조했고,
곡률이 음수로 더 작은 곳(더 들어간 곳)은 하늘색을 추가해줘서 강조햇다.



이제 volume 에서의 curvature를 확인해보자.
crag로 sdf volume을 만들어준다.
volume analysis 노드로 curvature에 대해 분석을 해주고, name 노드를 활용해서 이름을 바꿔준 뒤(curvature) primitive 노드의 volume tap에서 smoke로 볼 수 있도록 해준다.

분석에 방해되는 부분을 걷어내기 위해서 crag로 fog volume을 하나 더 만들어주고, 그것을 mask로 활용해서 위의 결과에 곱해주면, fog volume으로 만들어진 crag에 대한 부분만 남게된다.



밀도 정보를 시각화해보자(volume visualization)

현재 밀도처럼 보이지만, 곡률에 대한 정보이다.
곡률에 대한 값이 어떻게 구해졌을지는 아직은 알 수 없다.
- SDF로 curvature 값을 구했기 때문이다.
- 하지만, 어쨌든, 곡률정보이기 때문에 양수 / 음수 값을 가질 것이다.
양수 / 음수라고 해서 SDF가 아니다. 그냥 곡률의 양수 / 음수일 뿐이다.


곡률이 더 큰 곳의 강조를 위해 주황색을 추가해주고,
곡률이 더 작은 곳의 강조를 위해 하늘색을 추가해줬다.


curvature에 대해 오차가 있을 수 있다.
해상도에 따라 비슷한 모양일지라도 curvature 값의 폭이 바뀔 수도 있다.
- 어떤 때는 +/- 3 사이에 curvature가 형성될 때도 있지만, 어떤 때는 +/- 30 으로 폭이 바뀔수도 있다.
- 그래서, 해상도는 그때 그때 작은 값은 얼마가 나오는지, 큰 값은 얼마가 나오는지 확인할 필요가 있다.


volume에서의 curvature 범위는 생각보다 min / max의 범위가 크다는 것을 인지할 필요가 있다
상황파악.
우리가 현재 보고있는 curvature는 어디의 내용일까?


volume에서의 curvature field는 SDF가 같은 곳, Isovalue가 같은 곳에서의 curvature 값들을 보여주는 볼륨공간이다.
Curvature
- 곡률에 대한 정보
- 밖으로 튀어나온 느낌의 부분이 양수 / 안으로 들어간 느낌의 부분이 음수
- 많이 꺾이면 curvature의 크기가 커진다.
- 적게 꺾이면 curvature의 크기가 작아져서 0에 가까워진다.
여기까지는 폴리곤과 볼륨 모두 같은 내용이다.
- volume에서의 curvature field는 SDF가 같은 곳을 면으로 만들었을 때 그때의 곡률이 공간상에 볼륨정보로 다 저장되는 것
vector volume
vector volume의 시각화
curl noise - SDF를 함께 사용할 수 있는 noise
volume의 분석 - volume analysis, VDB analysis
gradient - vector 정보, SDF가 커지는 방향을 구한 것, volume의 노멀처럼 활용이 가능하다.
curvature - 곡률
아... 오늘 머리 터진다...
시각화하게 되는 정보들을 어떻게 활용할 수 있을지 고민을 하면서 수업을 듣긴 했는데, volume에서의 곡률에서 음...
음음... 음음음...
후디니 좀 더 만져봐야겠다.
volume blend
blend cd density cd alpha
'Houdini > Houdini1_Volumes' 카테고리의 다른 글
| 06_SOLVER와 함께 VOLUME 다루기 (1) | 2023.02.25 |
|---|---|
| 05_볼륨의 확산? 이류? VOLUME ADVECT (0) | 2023.02.22 |
| 03_VOLUME_part2. Volume 계산능력 향상 필수 (0) | 2023.02.17 |
| 03_VOLUME_part1. Volume 계산 Wrangle, Vop & Volume Sample, 구름 (0) | 2023.02.16 |
| 02_VOLUME NODE 다루기 & 시각화 (0) | 2023.02.15 |



